Fold a Regular Pentagon

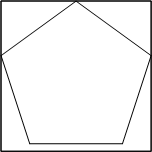
A square and a pentagon seem to inhabit different worlds. The square's right angles seem incompatible with the pentagon's interesting shape. At first glance it doesn't seem likely that you could fold one from the other. The saying "You can't get there from here." comes to mind. Yet, through a shared connection with the golden mean, you can create a regular pentagon from a square piece of paper.

Steps

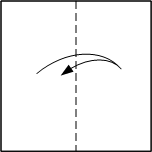Fold a square piece of paper in half. Open.
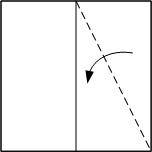Fold a diagonal of the right half.
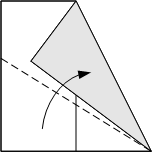Fold the bottom edge up so it lines up with the last crease.
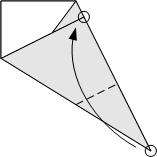Fold along the existing crease line so the point touches what was the bottom left corner of the paper. Open.
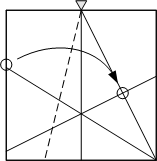Fold the paper so that the crease goes through the top middle of the paper and the left edge of the paper touches the intersection of the two creases in the right half of the paper.
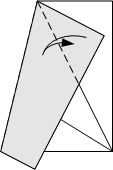Fold the corner of the paper back along the crease line on the paper below it. Open the paper.
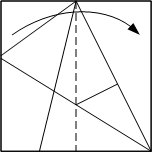Fold the paper in half again.
Fold along the previous crease.
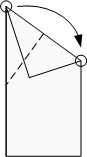Fold the new crease in half.
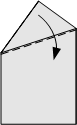Fold down along the edge of the paper.
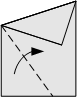Fold so the right-hand edge lines up with the edge.
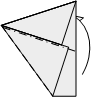Fold a mountain fold where the edges meet, folding the lower part back behind the upper part.
Fold a sharp crease along the edge of the paper shown. This crease will be the pentagon.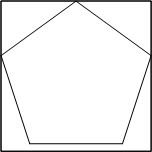
Open the paper to see a pentagon.

Notes

This sequence of folds capitalizes on the fact that the ratio of the diagonal of a pentagon to the edge is the golden mean (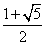) . The first five steps create a line segment of the proper length. The remaining steps copy this segment to their proper locations around the pentagon.
Assuming the square is 2 units wide, each side of the pentagon needs to be 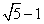units long. To get this value, solve the proportion mentioned above: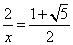
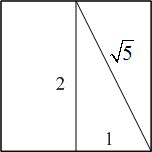
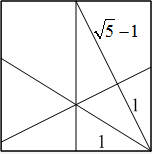The crease created in step 2 is the square root of 5 units long. Step 4 marks a point 1 unit along that crease. The remainder is a segment of the correct length.
There is an easier way to fold an approximately regular pentagon starting with an A4 piece of paper. This method relies on the fact that an A4 page is the square root of two times as long as it is wide. Folding opposite corners together creates a crease at an angle of 54.7° (the inverse tangent of the square root of two) which is close to the 54° angle that can be used to build a pentagon.