Interesting things to make out of paper—from mathematical models to toys.

• Browse
• Random
• About

Turn an Equilateral Triangle into a Square

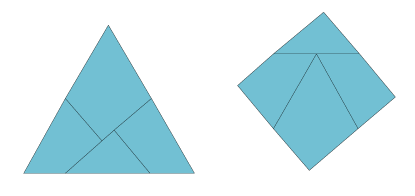
A classical puzzle in recreational math is to dissect a shape into pieces that can be rearranged into another shape. In this project you can turn an equilateral triangle into a square. If you cut out the pieces along the lines in the pattern you can rearrange them to form a square. In this case the rearrangement can be done by essentially turning the shape inside out. If you put hinges on three of the four places where the lines meet the edges of the triangle, the whole shape can be turned inside out while the hinges keep all the pieces connected.

Steps

1. Cut out the shape from the pattern.
   
2. Cut along the interior lines but note that in only one place do you cut through the tab. The other three tabs will act as hinges.
   
3. Fold the tabs up so they point straight up, i.e. perpendicular to the triangle.
   
4. Turn the triangle inside out to form a square. You might need to slightly adjust the folds that make up the "hinges" on this model. Small inaccuracies in cutting or folding make it so the square doesn't quite fit together as nicely as it should.
   

Notes

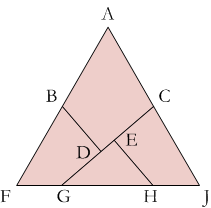• Here is how you can construct the pattern yourself. The trickiest part of making this pattern is to determine where points G and H should go. Points B and C are easy—they are the midpoints of the sides of the triangle. D and E are placed to make right angles that will form the corners of the square.
  If you notice how the pieces line up to make a square, you will see that FG and HJ abut GH so, FG + HJ = GH. This means that GH is half the side length.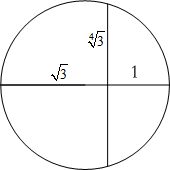
  
• I think it is easier to construct the lines of dissection than to calculate them. Assume the sides of the triangle are 2 units long. Its height is √3 units and its area is √3 units². Since this is also the area of the square, each side of the square is the fourth root of 3 (the square root of the square root of 3) units long. You can construct this length by constructing the square root of the height of the triangle.
  
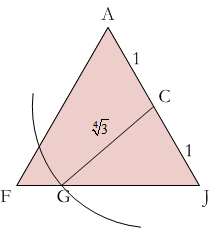• Draw a circle with this radius at C to find point G.
  
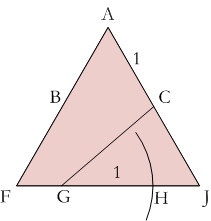• Draw a circle of radius 1 from point G to find H. Finish the construction by constructing perpendicular lines from B and H to the line GC.
  
  
• If you want to calculate the lengths of FG, GH and HJ, the ratio of FG : GH : HJ is approximately 0.491 : 1 : 0.509.
  

Links

• MathWorld has other interesting dissections
• Here is an animation of the hinged dissection

Comments

  © Laszlo Bardos