Dragon Curve

The dragon curve is a fractal curve that you can easily fold out of paper. In the image above, four dragon curves are placed together to show how they tile the plane. John Heighway discovered this curve that is sometimes called the Heighway dragon.
Steps
- Cut eight strips of paper, two strips of each of the four colors. I made strips 1 inch wide (2.5 cm) by 11 inches long.
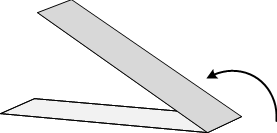 Fold a strip in half by bringing the right edge on top of the left edge.
Fold a strip in half by bringing the right edge on top of the left edge. 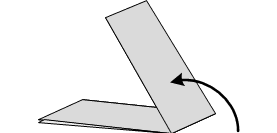 Fold the strip in half again right edge on top of left edge.
Fold the strip in half again right edge on top of left edge.  Fold the strip in half again two more times for a total of four folds always folding in the same direction.
Fold the strip in half again two more times for a total of four folds always folding in the same direction. 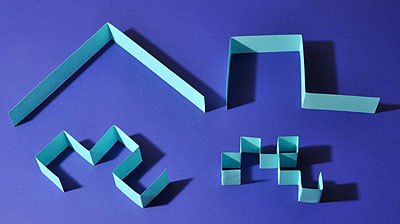 Unfold the strip of paper so that each fold is a right angle. This image shows what the strip of paper would look like if you opened it after the first fold, the second fold and so on. The shape in the lower right is what your strip of paper should look like.
Unfold the strip of paper so that each fold is a right angle. This image shows what the strip of paper would look like if you opened it after the first fold, the second fold and so on. The shape in the lower right is what your strip of paper should look like. Fold another curve and tape the two curves together as shown. Repeat for the other three colors.
Fold another curve and tape the two curves together as shown. Repeat for the other three colors.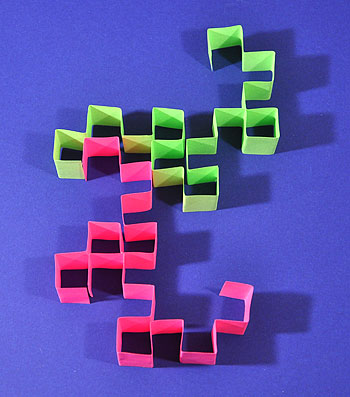 Place two curves together.
Place two curves together.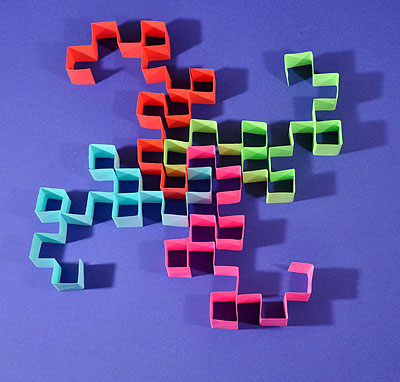 Add the remaining two curves to the pattern. Each curve starts at the same point but is rotated 90°.
Add the remaining two curves to the pattern. Each curve starts at the same point but is rotated 90°. You can extend the curves by cutting and folding two more strips of each color and adding them to the pattern as shown.
You can extend the curves by cutting and folding two more strips of each color and adding them to the pattern as shown.
Links
- Wikipedia's article on dragon curves includes an animated GIF showing the development of the fractal curve after each itteration. After about 10 itterations, you can see the dragon-like shape that gives this curve its name.
Comments
comments powered by Disqus
