Interesting things to make out of paper—from mathematical models to toys.

• Browse
• Random
• About

Moiré Ellipses and Hyperbolas from Circular Grids

Moiré patterns are formed by intersections of two grids of closely spaced lines or circles. Two copies of a circular grid offset from each other produce elliptical and hyperbolic patterns.

Materials

• Printable overhead transparency sheets. A copy shop can print these for you if you don't have transparencies. Or, as a last resort, you can simply print the pattern onto regular paper and hold these up to the light.
  

Steps

1. Print out the circular grids. onto an overhead transparency sheet.
   
2. Cut the page in half.
   
3. Overlap the two circular grids so the centers are offset. Observe the hyperbolas and ellipses formed.
   

Notes

• These moiré patterns illustrate how the radio-based navigation system LORAN works. A ship receives signals from stations that send out a synchronized radio signal. It calculates the time difference between signals from two stations. The ship can determine that it is somewhere along a hyperbolic path with the two stations at the foci. This is because a hyperbola is the set of points where the difference of the distances to two fixed points is constant. The ship repeats the calculation with another pair of stations and finds another hyperbola. The ship can determine its position as the intersection of the two hyperbolas.
  
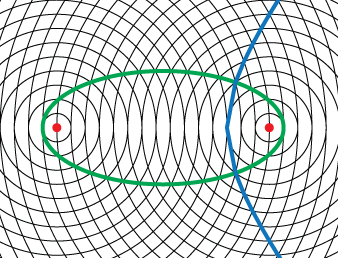• To prove that the patterns are ellipses, use the following definition of an ellipse: an ellipse is the set of all points whose distances to two fixed points sum to a constant. Since neighboring intersections of the moiré pattern are one unit farther away from one focus and one unit closer to the other, these intersections form an ellipse. Likewise, use the difference of distances to prove that the other patterns are hyperbolas.
  

References

• (Cullen 1990, 373)

Comments

  © Laszlo Bardos