Moiré Conic Sections from Linear and Circular Grids

Moiré patterns are patterns formed by overlapping grids of lines or circles. You can see moiré patterns on a TV or computer screen, for example, when it displays images of closely spaced lines. Lines from the image interact with scan lines from the display to create moiré patterns.
If you overlay a grid of lines with a grid of circles, the patterns of light and dark shapes are conic sections. In this project you will create parabolas, hyperbolas, and ellipses, depending on the line spacing.

Materials

Printable overhead transparencies

Steps

Print the pattern onto an overhead transparency sheet. (Copy shops can do this for you if you don't have a transparency that works in your printer.)
Cut out the grids.
Place the circular grid over the lines to make moiré patterns of the conic sections. If the lines are spaced the same distance apart as the circles, the pattern yields parabolas. If the lines are closer together than the circles, they result in hyperbolas. Finally, if the lines are farther apart, you get ellipses.

Notes

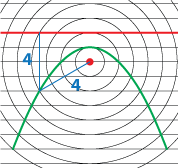You can prove that the moiré patterns are conic sections using a concept of eccentricity (e). Conic sections are the set of all points whose distance to a fixed point (f) is e times the distance to a fixed line (l). Parabolas have an e = 1. (This leads to the familiar definition of a parabola as a set of points equidistant to a point and a line.) Your eye connects points of intersections to form the curves. If the circular grid and the linear grid have the same spacing, the ratio of f/l is equal to one and the moiré pattern is a parabola.
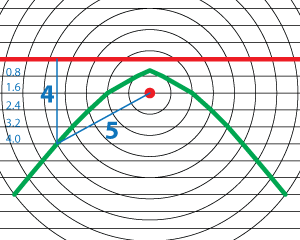Ellipses have an eccentricity between 0 and 1 and hyperbolas have e > 1. Since the lines in this grid are closer together than the circles, the moiré pattern is a hyperbola. The ratio of f to l is greater than one.