12-Celled Collapsoid

Jean Pedersen discovered convex polyhedra that she calls collapsoids while exploring a new way to make zonohedra (e.g. the rhombic dodecahedron and triacontahedron) out of pyramids. Her children played with an unfinished model of hers and discovered that it folds up. This 12-celled model has two variants that fold up in different ways.

Steps

1. Cut out 12 copies of the pattern piece from paper.
   
2. Score, fold and glue the pieces to form 12 baseless pyramids.
   
3. Tape six pyramids together in a row by their edges.
   
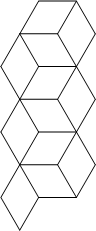4. Tape the remaining pyramids to the row of six pyramids as shown. The bases of the pyramids will distort to form rhombi.
   
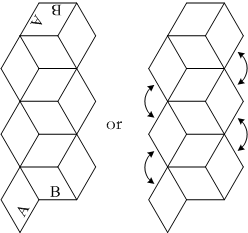5. Tape the edges using one of the two different options shown here. The first option will allow the collapsoid to flatten from two ends to make a hexagon (shown in the inset on the left in the top photo). The second option will allow the collapsoid to "unroll" to make two-thirds of a hexagon (inset on the right).
   

References

• (Pedersen, 1975)