Pattern
See also
Difficulty: 
Hyperbolic Paraboloid and Plücker's Conoid
A hyperbolic paraboloid (on the right) is a beautiful curve that has hyperbolic cross-sections horizontally and parabolic cross-sections vertically. Yet the strings that make up this shape all form straight lines.
If you use the same base, but thread the string differently, you can create a model of Plücker's conoid, another ruled surface.
Materials
- A cylindrical cardboard container about 3¾ in. (9.5 cm.) in diameter. This seems to be a standard size for food packaging in the U.S. The above model was made from one Ovaltine container. You can scale the print of the PDF file if your cylinder is a different size than this.
- Embroidery thread.
- Craft knife.
Steps
- Tape the patterns together and then onto the cardboard cylinder.
- Cut the cylinder in half along the sine wave with a craft knife.
- Make small slits in the cardboard at each mark. Remove the pattern from the cardboard cylinder.
- Tape the end of the thread to the cardboard container near the lowest slit on the curve.
- Stretch the thread from the slit in the valley to the one on the top of the hill.
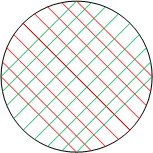Slip the thread into the next slit farther away from the first slit and stretch the thread across the container. The string should make a checkerboard pattern when viewed from above.- Continue until you reach the next mountain-valley pair.
- Use a different color thread and repeat, this time connecting different mountain-valley pairs.
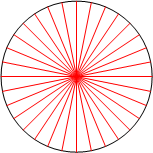To make the conoid stretch the string from one slit to the slit directly opposite it. From above, the strings forming the conoid look like spokes of a wheel.
Notes
- Fischer describes the formulas governing these shapes. Construct a curve
on cylinder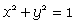 
. With string create line segments PQ and PQ' where 
, 
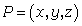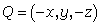, and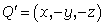 
to create a hyperbolic paraboloid with the equation 
.
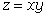Connect points P with P' where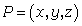 and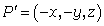 
to get Plücker's conoid with the equation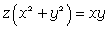 
References
Comments
comments powered by Disqus