Hyperboloid Haircut

Here is a novel way to create one part of a hyperboloid of two sheets.

Steps

1. Hang string of equal length from many points on a disk.
   
2. Collect the string to a point directly below the center of the disk.
   
3. Cut through the string at this point and let the string drop again. The string forms one branch of a hyperboloid of two sheets.
   

Notes

• Proof: If you cut at a point L units from the disk., each string will be cut to a length 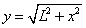(from the Pythagorean theorem.) Thus these ends form the equation of a hyperbola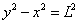
  

References

• (Alsina and Nelsen 2006, 131)