Double a Cube

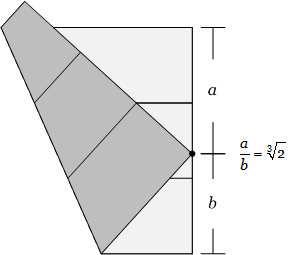
You can construct with origami. This is called "doubling a cube" because this is the dimensions of a cube with a volume twice as big as a unit cube, i.e., a volume of 2 cubic units. (To arrive at this number, take the cube root of both sides of the equation .)

Steps

1. Fold a square piece of paper into thirds.
   
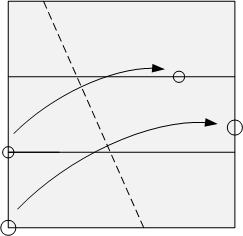2. Fold the paper so the bottom left-hand corner of the page touches the right edge at the same time as the bottom third touches the two-thirds line.
   
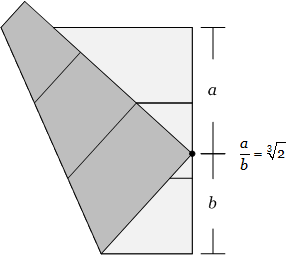3. The point where the corner touches the right edge of the page is the point where the ratio of the distance to the top of the page to the bottom is . So if a cube with a side length of "a", will have twice the volume of a cube of side length "b".
   

Notes

• Peter Messer discovered this origami cube-doubling in 1986.
  
• You can solve any cubic equation with origami as long you can construct the coefficients. This was proven by Margherita Piazzolla Beloch in 1936, but independently "rediscovered" by three more mathematicians in 1989, 1995 and 2000.
  

References

• (Demaine and O'Rourke 2007, 288-9)(Hull 2006)