Net of an Oblique Circular Cylinder

Creating an oblique circular cylinder isn't as easy as it seems. At first you might think that you can make one by simply cutting off the ends of a tube at a slant. However, this produces a cylinder with ellipses as bases, not circles. Creating the net of an oblique circular cylinder took some heavy mathematics.

Steps

1. Cut out the pattern from card stock. Cut out two copies of the circle.
   
2. Glue the strip into a cylinder.
   
3. Fold the tabs down and glue the two circles onto the ends.
   

Notes

• The curvy sides of the net are not sine waves. They are a more complicated curve that requires elliptic integrals to calculate.
  
• To calculate the shape of the curve in this net, place a unit circle on the x-y plane and rotate it α degrees about the x-axis. Extend the cylinder up the z-axis. In this position, a horizontal cross-section of the cylinder is an ellipse with semimajor and semiminor axes of a= 1 and b = cos(α). This ellipse can be represented by the parametric equations .
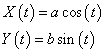  The height of the circle above the x-y plane is the height of the curve at any point along the perimeter of the ellipse. The height of the circle is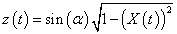 . The distance along the perimeter of the ellipse is given by the incomplete elliptic integral of the second kind .
  

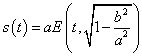References

• (Bardos 2009)