Hyperbolic Paraboloid

How is this for a groovy shape? This is a hyperbolic paraboloid, a saddle shape sometimes described as "Pringle" shaped after the potato chip brand. If you cut this shape horizontally, the cross-section would be a hyperbola. Vertical cross-sections are parabolas. The surprising thing about this shape is that can be made with straight lines.
Video Instructions
Materials
- Boxboard from a cereal box.
- Craft thread.
Steps
- Cut out a square from boxboard using the pattern (or any size you care to make).
- Cut evenly-spaced, short slits around the perimeter of the square.
- Score and fold the square along one diagonal.
- Cut a slot along the other diagonal that extends from the center of the square to a point about half-way to the corners.
- Slip a piece of boxboard into the slot that you just made to make a stand. You might need to widen the slot just a bit so the piece of boxboard fits without distorting the square.
- Adjust the angle of the folded square so it is close to 90°. The shape will be a hyperbolic paraboloid at any angle, but I think a right angle makes a pleasing shape.
- Tape the end of the thread to the underside of the square.
- String the thread from one slit to the slit directly across from it on the opposite side of the square. Viewed from above, the thread will form a checkerboard pattern.
- Continue around the square.
- Check for parabolic cross-sections using the parabolas from the pattern. Cut out the two parabolas, cut the slits, and slip them together at the slits. The two parabolas should be perpendicular to each other.
Notes
- You can derive the equation of this hyperbolic paraboloid as Gerd Fischer explains in his book:
The equation of a hyperbolic paraboloid is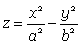 which can be written as parametric equations
which can be written as parametric equations 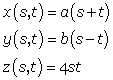
If you lay this model flat and set the y-axis to be along the crease and the x-axis along the other diagonal of the square, you can describe this with the parametric equations: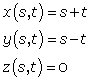 . Here the lines
. Here the lines 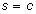 and
and 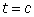 are the equations of the lines formed by the string in the model. As you raise the two halves of the model up an angle of Θ these equations become
are the equations of the lines formed by the string in the model. As you raise the two halves of the model up an angle of Θ these equations become 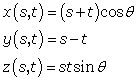 which is equivalent to
which is equivalent to 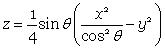 the equation of this hyperbolic paraboloid.
the equation of this hyperbolic paraboloid.
References
Comments
comments powered by Disqus
